树 是一种经常用到的数据结构,用来模拟具有树状结构性质的数据集合。
树里的每一个节点有一个根植和一个包含所有子节点的列表。从图的观点来看,树也可视为一个拥有N 个节点和N-1 条边的一个有向无环图。
二叉树是一种更为典型的树树状结构。如它名字所描述的那样,二叉树是每个节点最多有两个子树的树结构,通常子树被称作“左子树”和“右子树”。
叶子节点是指没有子节点的节点。
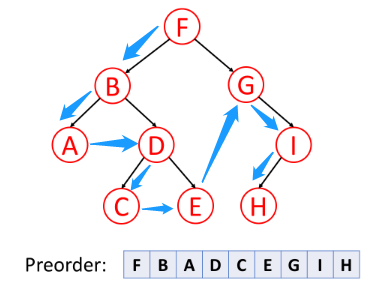
前序遍历
前序遍历首先访问根节点,然后遍历左子树,最后遍历右子树。
// 定义二叉树节点
function TreeNode(val) {
this.val = val;
this.left = this.right = null;
}
// 递归
function preorderTraversal(root) {
if (!root) {
return []
}
let res = []
res.push(root.val)
root.left && res.push(...preorderTraversal(root.left))
root.right && res.push(...preorderTraversal(root.right))
return res
}
// 迭代,利用栈先进后出
function preorderTraversal(root) {
if (!root) {
return []
}
let stack = [], res = []
while(root) {
res.push(root.val)
// 后遍历右子树,先入栈
root.right && stack.push(root.right)
// 先遍历左子树,后入栈
root.left && stack.push(root.left)
// 左子树出栈
root = stack.pop()
}
return res
}
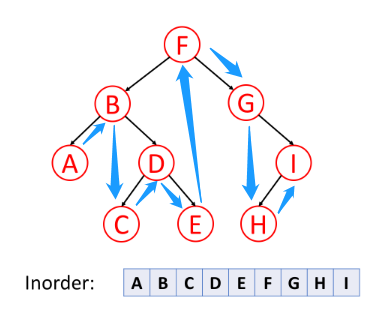
中序遍历
中序遍历是先遍历左子树,然后访问根节点,然后遍历右子树。
- 判断 left 节点是否存在,如果存在则进入 left 节点,并将当前点入栈
- 当 left 节点和 right 节点都为 null 时,则记录当前节点,通过栈返回上一节点,将上一节点 left 置为 null
- 当 left 节点为 null 且 right 节点存在时,则记录当前节点,然后跳到 right 节点
// 定义二叉树节点
function TreeNode(val) {
this.val = val;
this.left = this.right = null;
}
function inorderTraversal(root) {
let stack = [], res = []
while (root) {
if (root.left) {
stack.push(root)
root = root.left
} else if (!root.left && !root.right) {
res.push(root.val)
root = stack.pop()
root && (root.left = null)
} else if (root.right) {
res.push(root.val)
root = root.right
}
}
return res
}
function inorderTraversal(root) {
let stack = [], res = []
while (stack.length || root != null) {
while (root != null) {
stack.push(root)
root = root.left
}
root = stack.pop()
res.push(root.val)
root = root.right
}
return res
}
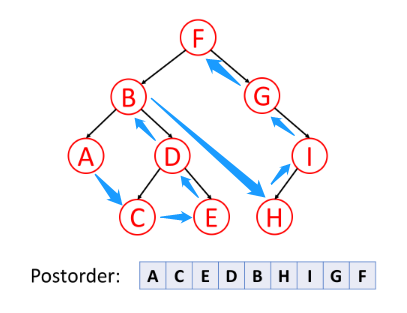
后序遍历
后序遍历是先遍历左子树,然后遍历右子树,最后访问树的根节点。
- 如果 left 节点存在,则遍历,直到末尾节点,才记录,然后返回上一节点
- 当子节点遍历完毕时,才记录当前节点
// 定义二叉树节点
function TreeNode(val) {
this.val = val;
this.left = this.right = null;
}
function postorderTraversal(root) {
let stack = [], res = []
while(root) {
if (root.left) {
stack.push(root)
root = root.left
} else if (root.right) {
stack.push(root)
root = root.right
} else {
res.push(root.val)
root = stack.pop()
if (root && root.left) {
root.left = null
} else if (root && root.right) {
root.right = null
}
}
}
return res
}
// 类似前序遍历方法
function postorderTraversal(root) {
let stack = [], res = []
while(root) {
res.unshift(root.val)
root.left && stack.push(root.left)
root.right && stack.push(root.right)
root = stack.pop()
}
return res
}
层序遍历
层序遍历就是逐层遍历树结构。
广度优先搜索是一种广泛运用在树或图这类数据结构中,遍历或搜索的算法。 该算法从一个根节点开始,首先访问节点本身。 然后遍历它的相邻节点,其次遍历它的二级邻节点、三级邻节点,以此类推。
当我们在树中进行广度优先搜索时,我们访问的节点的顺序是按照层序遍历顺序的。
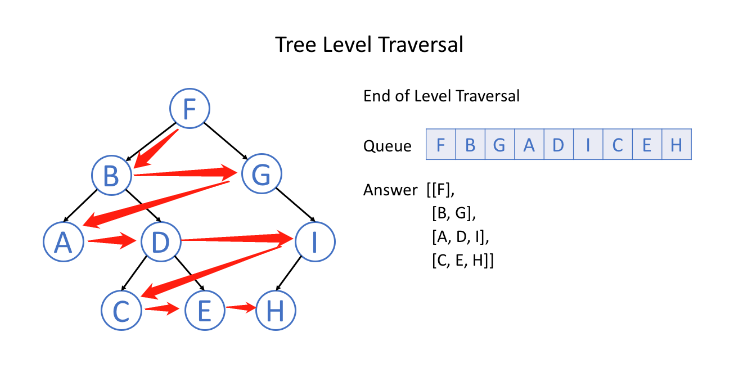
// 定义二叉树节点
function TreeNode(val) {
this.val = val;
this.left = this.right = null;
}
function levelOrder(root) {
let queue = [], res = []
if (root) {
queue.push(root)
}
while (queue.length !== 0) {
let arr = [], len = queue.length
for (let i = 0; i < len; i++) {
let currNode = queue.shift()
if (currNode.left) {
queue.push(currNode.left)
}
if (currNode.right) {
queue.push(currNode.right)
}
arr.push(currNode.val)
}
res.push(arr)
}
return res
}
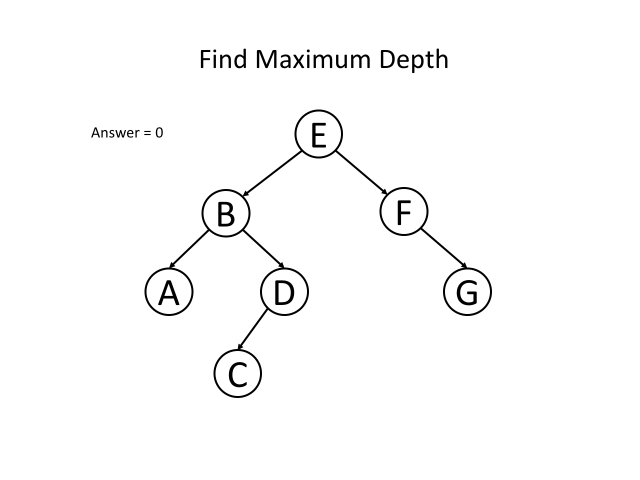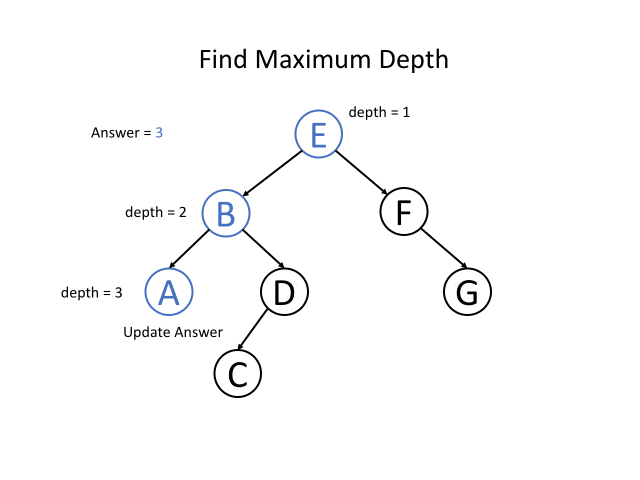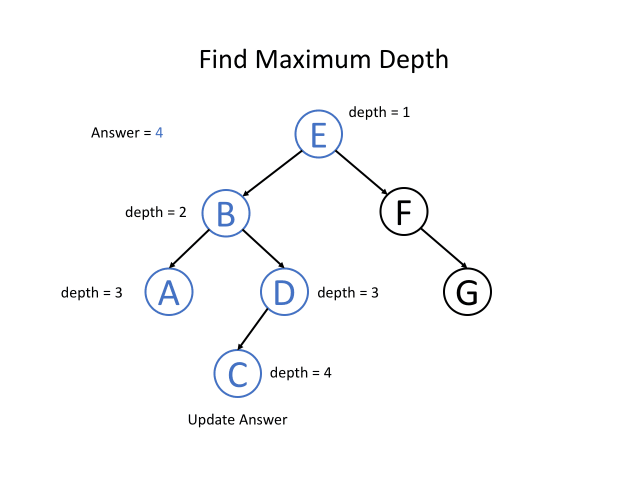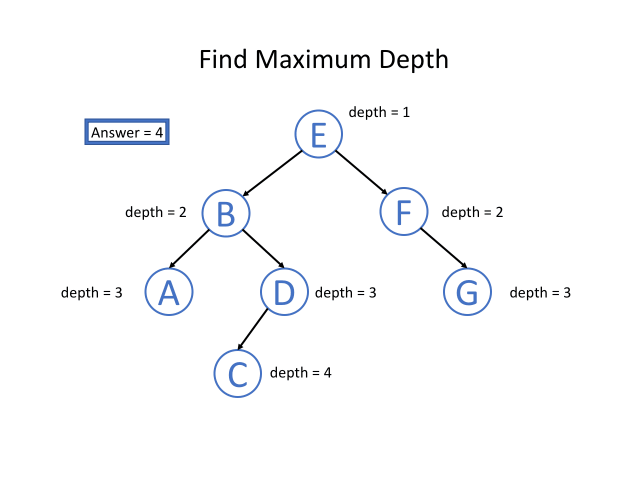
运用递归解决树的问题
“自顶向下” 的解决方案
“自顶向下” 意味着在每个递归层级,我们将首先访问节点来计算一些值,并在递归调用函数时将这些值传递到子节点。 所以 “自顶向下” 的解决方案可以被认为是一种前序遍历。
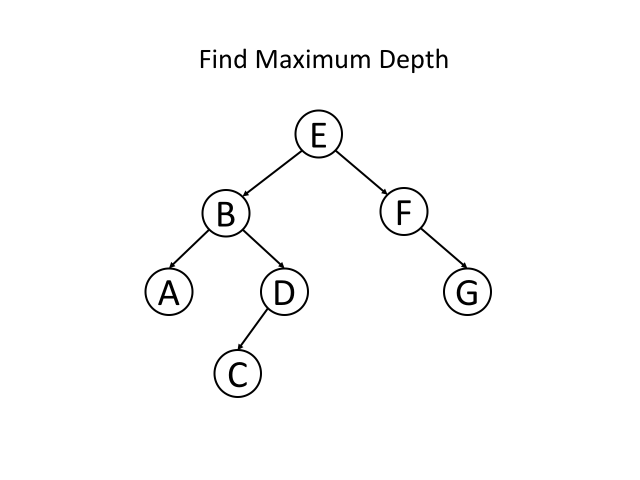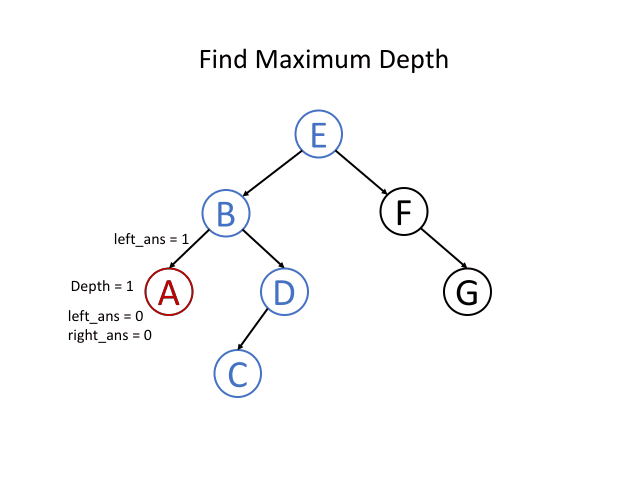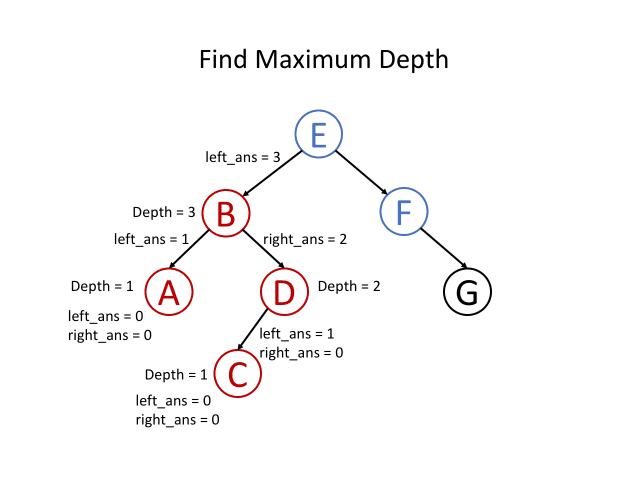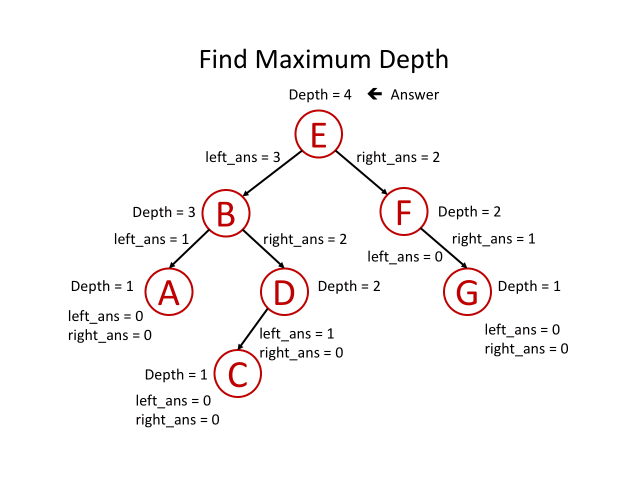
我们知道根节点的深度是1。 对于每个节点,如果我们知道某节点的深度,那我们将知道它子节点的深度。 因此,在调用递归函数的时候,将节点的深度传递为一个参数,那么所有的节点都知道它们自身的深度。 而对于叶节点,我们可以通过更新深度从而获取最终答案。
“自底向上” 的解决方案
“自底向上” 是另一种递归方法。 在每个递归层次上,我们首先对所有子节点递归地调用函数,然后根据返回值和根节点本身的值得到答案。 这个过程可以看作是后序遍历的一种。
如果我们知道一个根节点,以其左子节点为根的最大深度为l和以其右子节点为根的最大深度为r,我们是否可以回答前面的问题? 当然可以,我们可以选择它们之间的最大值,再加上1来获得根节点所在的子树的最大深度。 那就是 x = max(l,r)+ 1。 这意味着对于每一个节点来说,我们都可以在解决它子节点的问题之后得到答案。
总结
了解递归并利用递归解决问题并不容易。 当遇到树问题时,请先思考一下两个问题:
- 你能确定一些参数,从该节点自身解决出发寻找答案吗?
- 你可以使用这些参数和节点本身的值来决定什么应该是传递给它子节点的参数吗? 如果答案都是肯定的,那么请尝试使用 “自顶向下” 的递归来解决此问题。
或者你可以这样思考:对于树中的任意一个节点,如果你知道它子节点的答案,你能计算出该节点的答案吗? 如果答案是肯定的,那么 “自底向上” 的递归可能是一个不错的解决方法。
二叉树的最大深度
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
/**
* Definition for a binary tree node.
* function TreeNode(val) {
* this.val = val;
* this.left = this.right = null;
* }
*/
/**
* @param {TreeNode} root
* @return {number}
*/
var maxDepth = function(root) {
let depth = 0, queue = []
if (root) {
queue.push(root)
}
while(queue.length !== 0) {
depth += 1
let len = queue.length
for (let i = 0; i < len; i++) {
let currNode = queue.shift()
if (currNode.left) {
queue.push(currNode.left)
}
if (currNode.right) {
queue.push(currNode.right)
}
}
}
return depth
};
重建二叉树
输入某二叉树的前序遍历和中序遍历的结果,请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。 例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6},则重建二叉树并返回。
/* function TreeNode(x) {
this.val = x;
this.left = null;
this.right = null;
} */
function reConstructBinaryTree(pre, vin)
{
if (pre.length === 0 || vin.length === 0) {
return []
}
let node = new TreeNode(pre[0])
let i = 0
for (i; i < pre.length; i++) {
if (pre[i] == node.val) {
break
}
}
node.left = reConstructBinaryTree(pre.slice(1, i+1), vin.slice(0, i))
node.right = reConstructBinaryTree(pre.slice(1+1), vin.slice(i+1))
return node
}
深度优先遍历 (DFS)
Depth-First-Search
广度优先遍历 (BFS)
Breadth-First-Seach
二叉搜索树
二叉搜索树(BST)是二叉树的一种特殊表示形式,它满足如下特性:
- 每个节点中的值必须大于存储在其左侧子树中的任何值。
- 每个节点中的值必须小于存储在其右子树中的任何值。